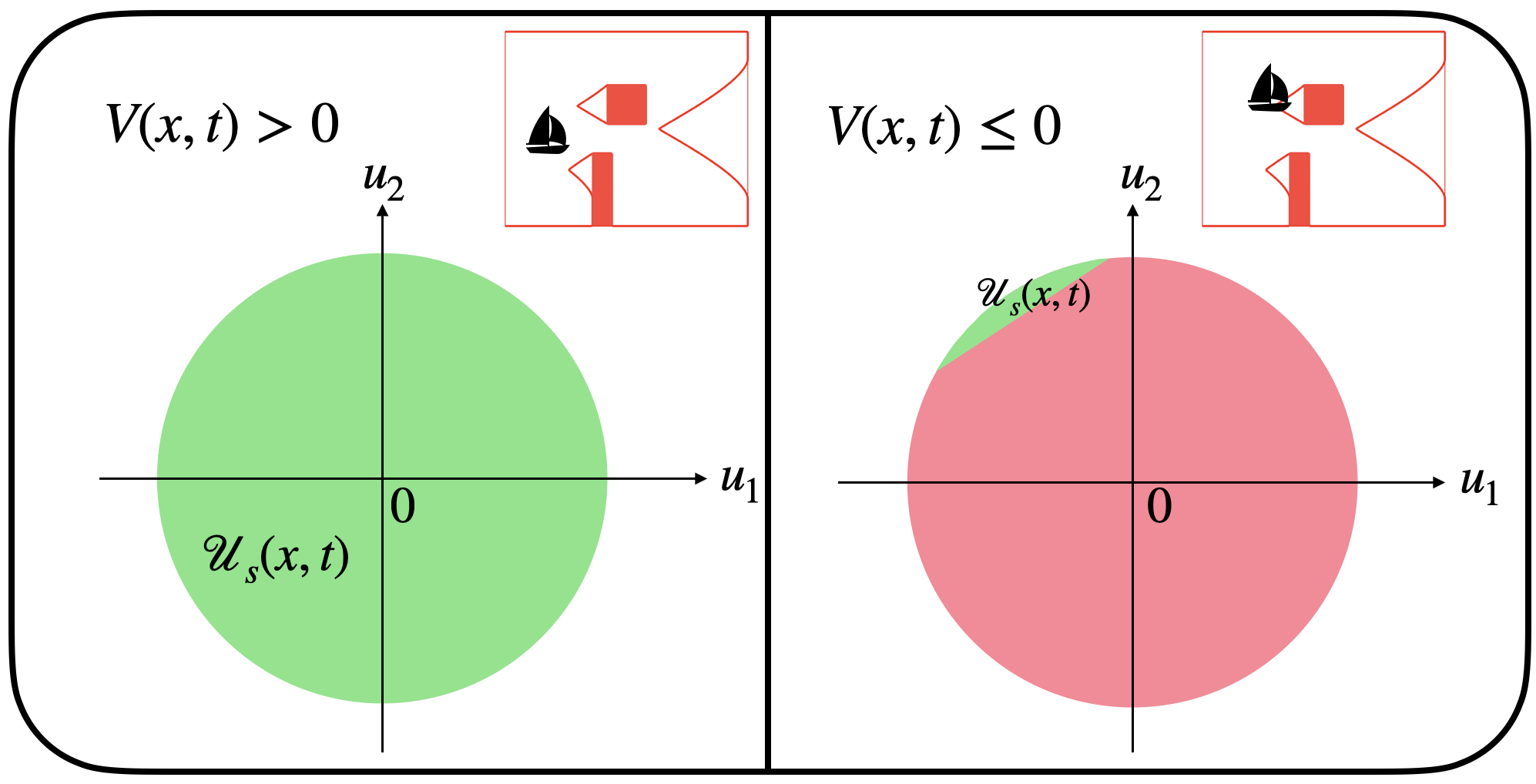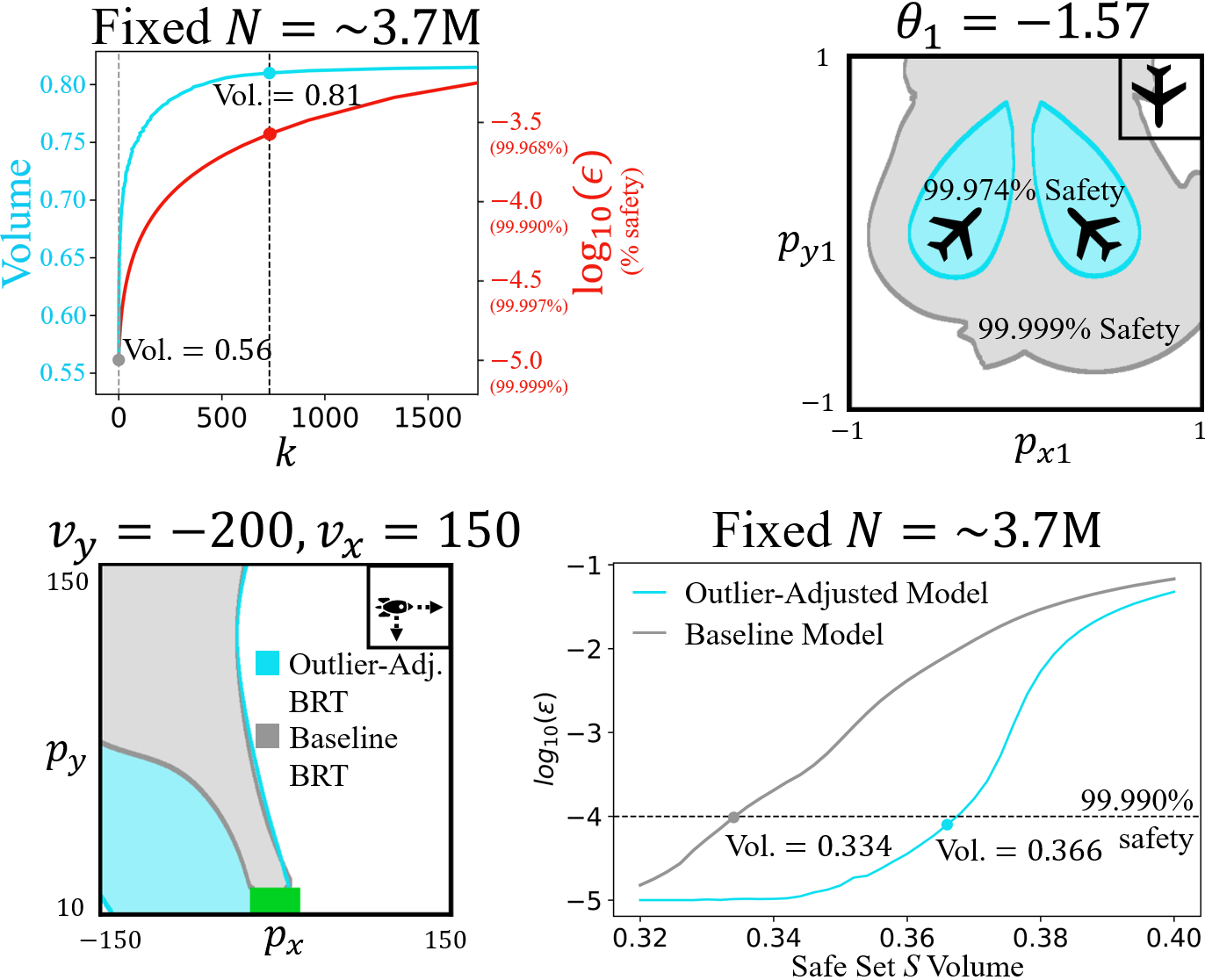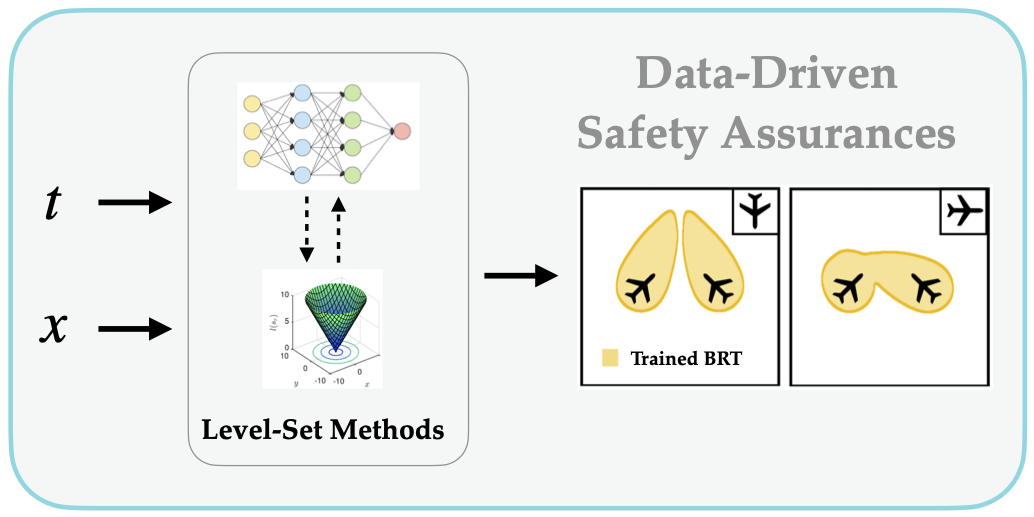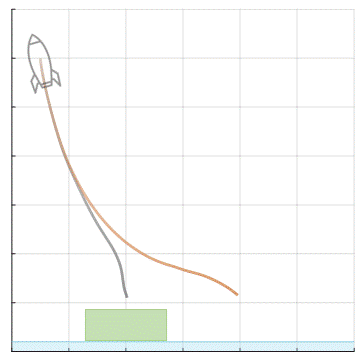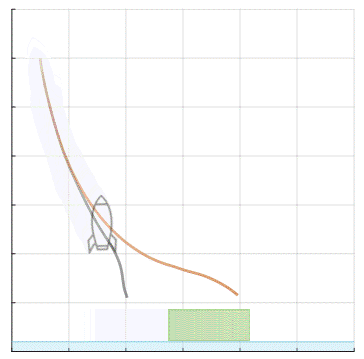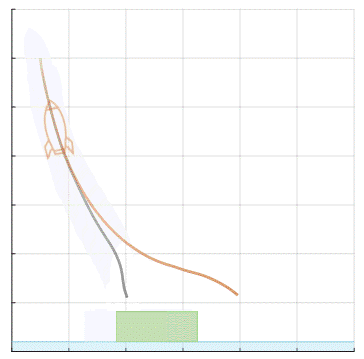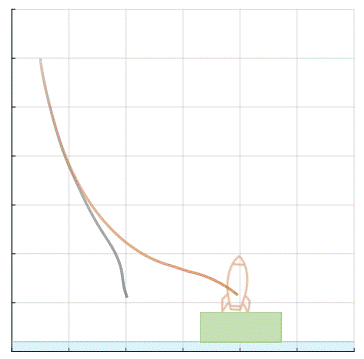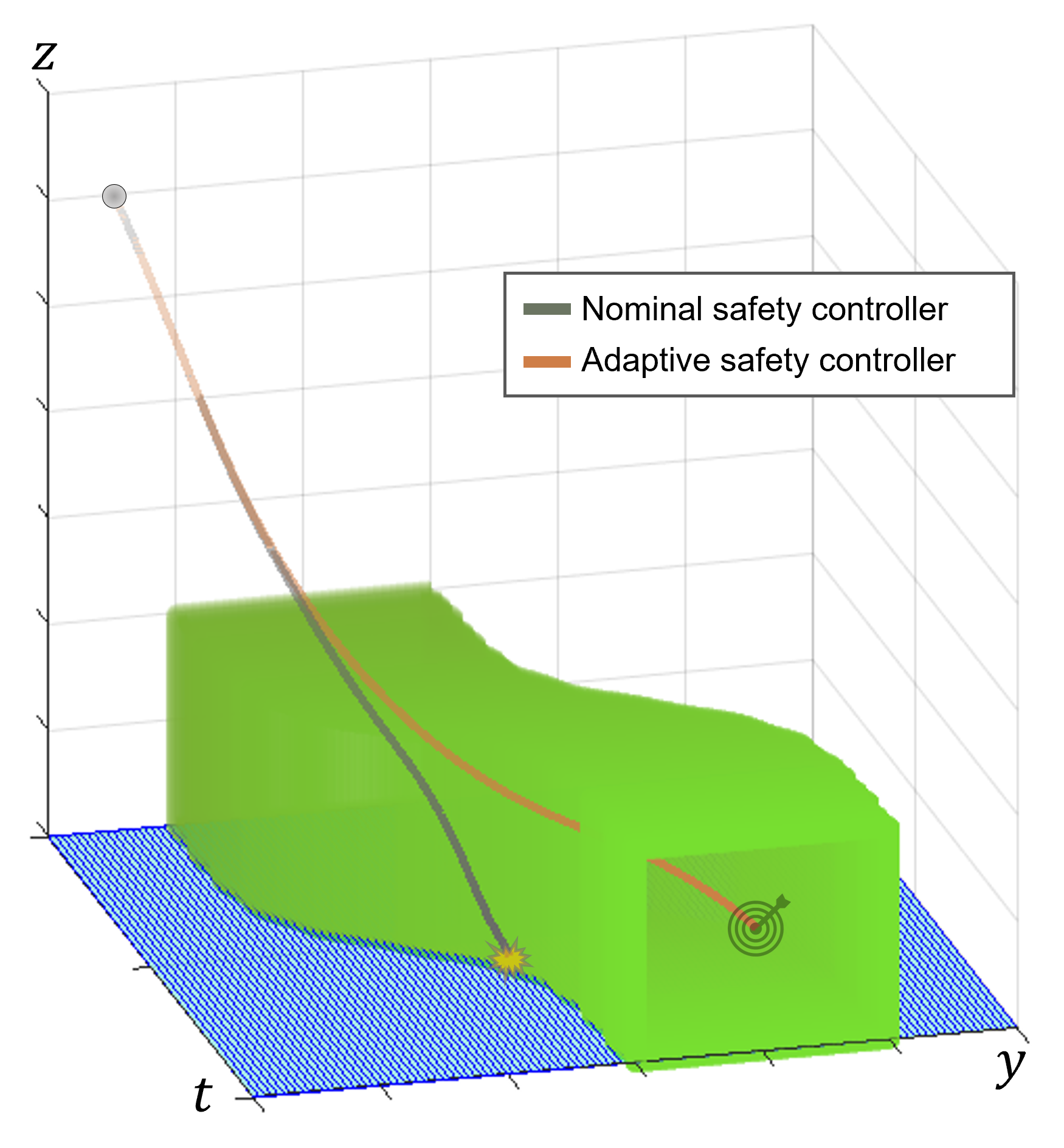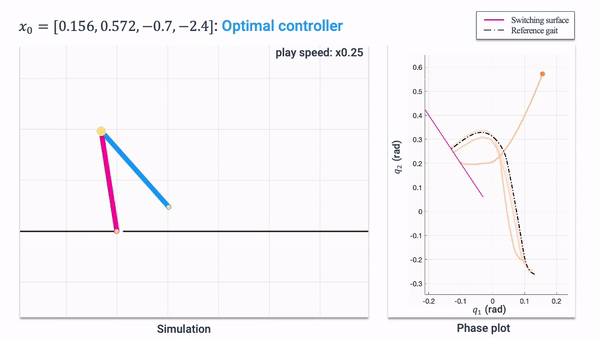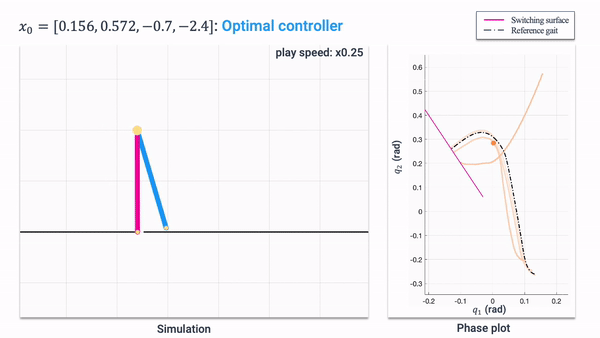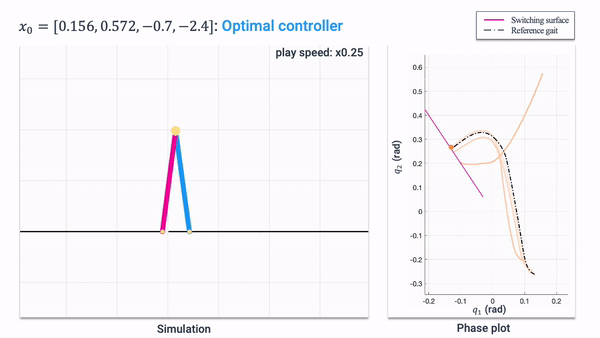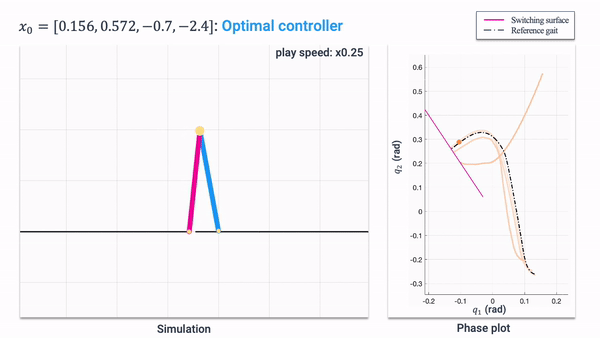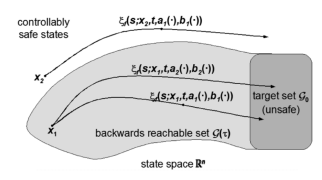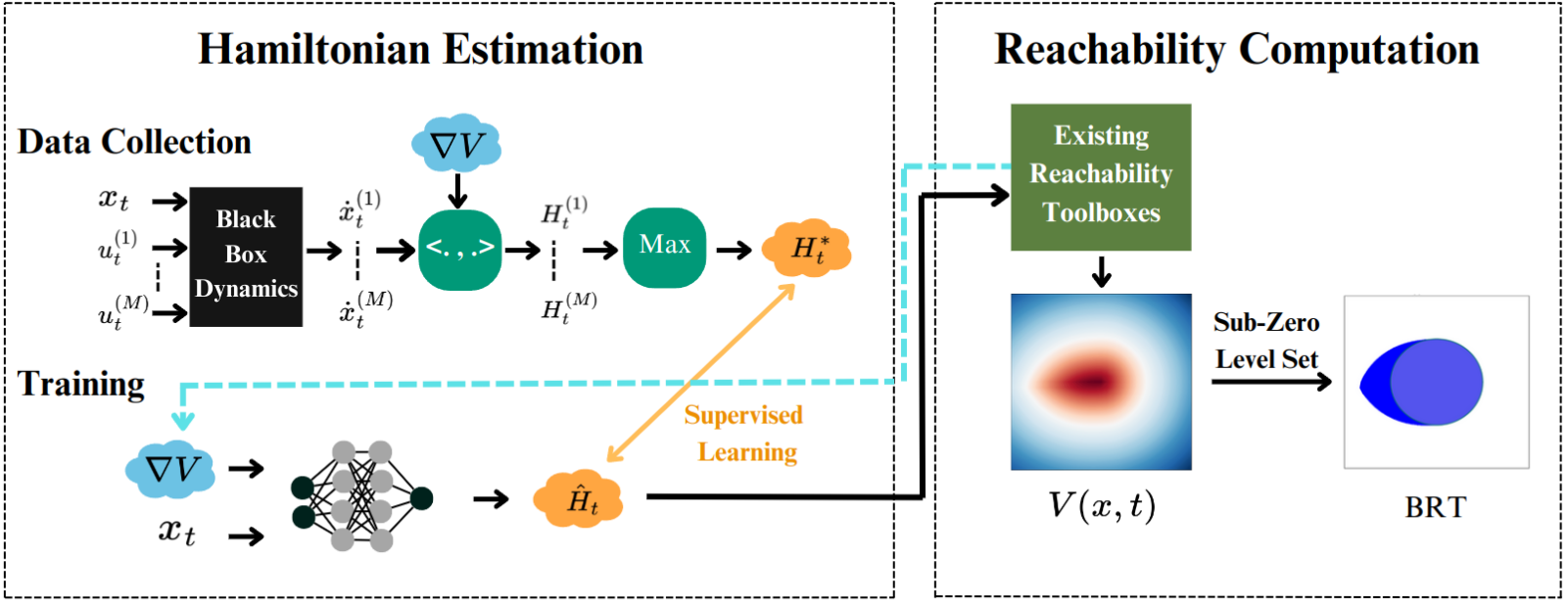
Hamilton-Jacobi (HJ) reachability analysis is a powerful framework for ensuring safety and performance in autonomous systems. However, existing methods typically rely on a white-box dynamics model of the system, limiting their applicability in many practical robotics scenarios where only a black-box model of the system is available. In this work, we propose a novel reachability method to compute reachable sets and safe controllers for black-box dynamical systems. Our approach efficiently approximates the Hamiltonian function using samples from the black-box dynamics. This Hamiltonian is then used to solve the HJ Partial Differential Equation (PDE), providing the reachable set of the system. The proposed method can be applied to general nonlinear systems and can be seamlessly integrated with existing reachability toolboxes for white-box systems to extend their use to black-box systems.

As autonomous systems become more complex and integral in our society, the need to accurately model and safely control these systems has increased significantly. In the past decade, there has been tremendous success in using deep learning techniques to model and control systems that are difficult to model using first principles. However, providing safety assurances for such systems remains difficult, partially due to the uncertainty in the learned model. In this work, we aim to provide safety assurances for systems whose dynamics are not readily derived from first principles and, hence, are more advantageous to be learned using deep learning techniques. Given the system of interest and safety constraints, we learn an ensemble model of the system dynamics from data. Leveraging ensemble uncertainty as a measure of uncertainty in the learned dynamics model, we compute a maximal robust control invariant set, starting from which the system is guaranteed to satisfy the safety constraints under the condition that realized model uncertainties are contained in the predefined set of admissible model uncertainty.

Hybrid dynamical systems with nonlinear dynamics are one of the most general modeling tools for representing robotic systems, especially contact-rich systems. However, providing guarantees regarding the safety or performance of nonlinear hybrid systems remains a challenging problem because it requires simultaneous reasoning about continuous state evolution and discrete mode switching. In this work, we address this problem by extending classical Hamilton-Jacobi (HJ) reachability analysis, a formal verification method for continuous-time nonlinear dynamical systems, to hybrid dynamical systems. We characterize the reachable sets for hybrid systems through a generalized value function defined over discrete and continuous states of the hybrid system. We also provide a numerical algorithm to compute this value function and obtain the reachable set. Our framework can compute reachable sets for hybrid systems consisting of multiple discrete modes, each with its own set of nonlinear continuous dynamics, discrete transitions that can be directly commanded or forced by a discrete control input, while still accounting for control bounds and adversarial disturbances in the state evolution. Along with the reachable set, the proposed framework also provides an optimal continuous and discrete controller to ensure system safety.

Autonomous systems have witnessed a rapid increase in their capabilities, but it remains a challenge for them to perform tasks both effectively and safely. The fact that performance and safety can sometimes be competing objectives renders the cooptimization between them difficult. One school of thought is to treat this cooptimization as a constrained optimal control problem with a performance-oriented objective function and safety as a constraint. However, solving this constrained optimal control problem for general nonlinear systems remains challenging. In this work, we use the general framework of constrained optimal control, but given the safety state constraint, we convert it into an equivalent control constraint, resulting in a state and time-dependent control-constrained optimal control problem. This equivalent optimal control problem can readily be solved using the dynamic programming principle. We show the corresponding value function is a viscosity solution of a certain Hamilton-Jacobi-Bellman Partial Differential Equation (HJB-PDE).

Hamilton-Jacobi (HJ) reachability-based filtering provides a powerful framework to co-optimize performance and safety (or liveness) for autonomous systems. Under this filtering scheme, a nominal controller is minimally modified to ensure system safety or liveness. However, the resulting controllers can exhibit abrupt switching and bang-bang behavior, which is not suitable for applications of autonomous systems in the real world. This work presents a novel, unifying framework to design safety and liveness filters through reachability analysis. We explicitly characterize the maximal set of control inputs that ensures safety (or liveness) at a given state. Different safety filters can then be constructed using different subsets of this maximal set along with a projection operator to modify the nominal controller. We use the proposed framework to design three safety filters, each balancing performance, computation time, and smoothness differently. The proposed filters can easily handle dynamics uncertainties, disturbances, and bounded control inputs. We highlight their relative strengths and limitations by applying these filters to autonomous navigation and rocket landing scenarios and on a physical robot testbed. We also discuss practical aspects associated with implementing these filters on real-world autonomous systems. Our research advances the understanding and potential application of reachability-based controllers on real-world autonomous systems.

Learning-based approaches, such as DeepReach, have been used to synthesize reachable tubes and safety controllers for high-dimensional systems. However, verifying these neural reachable tubes remains challenging. In this project, we propose two verification methods, based on robust scenario optimization and conformal prediction, to provide probabilistic safety guarantees for neural reachable tubes. Our methods allow a direct trade-off between resilience to outlier errors in the neural tube, which are inevitable in a learning-based approach, and the strength of the probabilistic safety guarantee. Furthermore, we show that split conformal prediction, a widely used method in the machine learning community for uncertainty quantification, reduces to a scenario-based approach, making the two methods equivalent not only for verification of neural reachable tubes but also more generally. To our knowledge, our proof is the first to reveal a strong relationship between conformal prediction and scenario optimization. Finally, we propose an outlier-adjusted verification approach that uses the error distribution in neural reachable tubes to recover greater safe volumes. We demonstrate the efficacy of the proposed approaches for the high-dimensional problems of multi-vehicle collision avoidance and rocket landing with no-go zones.

DeepReach, a reachability toolbox that leverages recent advances in neural PDE solvers to tractably solve high-dimensional reachability problems. The computational requirements of DeepReach do not scale directly with the state dimension, but rather with the complexity of the underlying reachable tube. DeepReach achieves comparable results to the state-of-the-art reachability methods, does not require any explicit supervision for the PDE solution, can easily handle external disturbances, adversarial inputs, and system constraints, and also provides a safety controller for the system.

Existing methods provide safety assurances under the assumption that once deployed, the system or its environment does not evolve. Online, however, an autonomous system might experience changes in system dynamics, control authority, external disturbances, and/or the surrounding environment, requiring updated safety assurances, which can be timeconsuming and often intractable to perform online. Assuming system and environment changes can be parameterized, we leverage recent advances in high-dimensional reachability analysis to compute parameter-conditioned reachable sets -- a family of reachable set parameterized by the uncertain system and environment factors. Online, as these factors change, the system can query the corresponding safety function from this family to ensure system safety, enabling a real-time update of the safety assurances.

Contact-rich robotic systems, such as legged robots and manipulators, are often represented as hybrid systems. However, designing stabilizing controllers for these systems is often challenging because of the discontinuous state changes upon contact (also referred to as state resets). In this work, we generalize the HJ reachability framework to account for the discontinuous state changes originating from state resets, which has remained a challenge until now. We apply our approach for computing region-of-attractions and stabilizing controllers for several underactuated walking robots and demonstrate that the obtained controllers can leverage the state resets and contacts for enhancing the system stability.

The tutorial covered the theoretical foundations as well as computational tools for Hamilton-Jacobi (HJ) reachability analysis. The tutorial facilitated the application of HJ reachability to a variety of research domains such as model validation, human-robot interaction, and bio-engineering; it also started a platform for collaboration between these different fields.